Obligatory post about Landauer's principle

Landauer's principle is a relationship between informational (logic) entropy and thermodynamic entropy. I have to disclaim, it's been challenged many times and no clear conclusion on its correctness exist yet.

any logically irreversible manipulation of information, such as the erasure of a bit or the merging of two computation paths, must be accompanied by a corresponding entropy increase in non-information-bearing degrees of freedom of the information-processing apparatus or its environment

Or, in layman's terms; a decrease in logic entropy (such as erasing bits of information) must come with an increase in another form of entropy, namely thermodynamic entropy, aka heat.

The wikipedia page is much clearer than I could ever be about the exact physics, but I'd like to share a thought experiment that might convince you (or not, feel free to discuss) of the validity of Landauer's principle, or just introduce you to some nice trivia.

Maxwell's Demon

Maxwell's demon (top) monitors the individual speed and positions of all the particles at any given point in time. Two thermally isolated compartments A and B are separated by a small door (that can be opened and closed reversibly, meaning that it can be done without expending any energy overall). While particles in A and B have average velocities equal to each room's temperature, we can quantify that some of them are going faster or slower with a Maxwell-Botlzmann distribution.

When the demon sees in room A (at T1 temp) a particle that's going faster than a threshold, and there's going to be some eventually, it opens the door to let the high-energy particle through to B (at temp T2). Similarly, it lets slower "cold" particles go from B to A, effectively creating energy from nothing because a temperature difference can be used to create useful work, with adapters such as a turbine or a Peltier module (or anything, really).

The global thermodynamic entropy of the system also decreases, violating the second law of thermodynamics, but even staying down-to-earth, creating energy from nothing does not sounds right.

The demon is the outlier here. There is no lower bound of energy consumption from the actuation of the door. There should not be lower bound of energy consumption for observing the particles, and while heisenberg's lurks dangerously close, we don't actually need high precision. So maybe it's computing all the data that requires, fundamentally, energy ? Computers do need energy, sure, but can't we just make computing more efficient to the extent we could power the computer with the energy we collect from exploiting the temperature difference ? That may will require a paradigm shift from the current semiconductor-based mainframes, but quantum is here, people.

The demon isn't god

The demon, or in our precise case, the computer, is a finite piece that has a limited amount of memory. Therefore, at some point the demon/computer will have to erase 'old' data from memory to make place for new data.

The demon's algorithm should work basically like this:

• Measure all A & B room particles speed and position at time t
• Predict the evolution of the energy difference between the rooms at t + Δt should the door be opened, that will change because some particles will cross.
• If the difference of temperature increases, do open the door. Else let it closed.
• Erase/free the memory used to store speed and positions (because it doesn't have infinite memory)

In practice, the first and last steps might be joined into one that 'overwrite' previous data or you can do one particle at the time and sum it in the 'loop'... feel free to optimize. But the fact is, we erase information. We decrease the logic entropy of the system. Wait. There's no 2nd law of thermodynamics for logic entropy. Should there be one ?

The solution

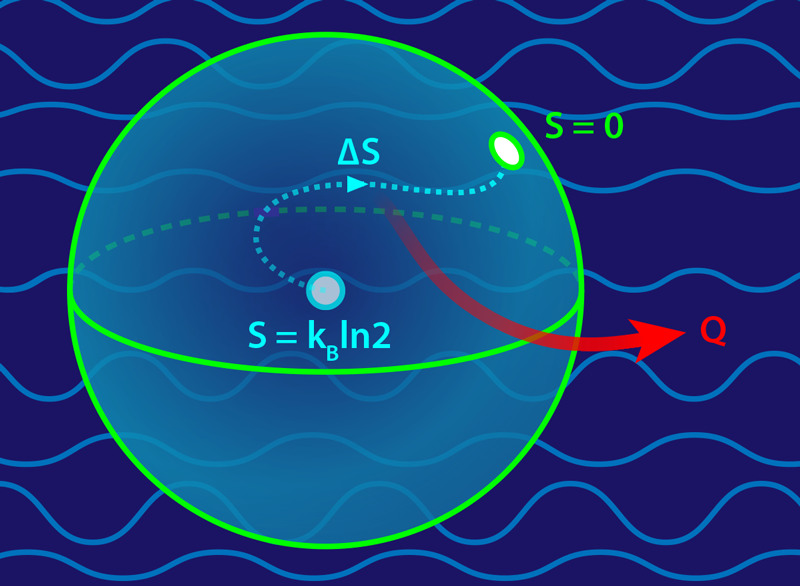
Landauer solves this by (oversimplified) saying that logic and thermodynamic entropy are two sides of the same coin, and that overall entropy shall not decrease. A decrease in logic entropy must therefore be accompanied by an increase in thermodynamic entropy.

In numbers, Landauer's principle states a lower bound of energy to erase a bit of at least :

At room temperature, that's about 0.0175 eV. Not much, though nowadays computer easily write at 50GB/s to their L1 cache, times 8 cores of some imaginary CPU. Logic entropy thus contribute to around 3 nW (nanoWatts) of the 50W total guesstimated TDP. Not much, but still... it's not nothing.

bonus notes:

• Landauer's principle also solves the Gibbs paradox
• If Koomey's law holds true (unlikely), we'll have to take into account Landauer's limit when crafting algorithms (erasing less data, in a "reversible" fashion) by 2050. Early!